并查集(Disjoint Set)

并查集接口（方法）

  • connect(x,y)：将x，y元素连接起来。（连接具有传递性）

  • isConnected(x,y)：判断x，y元素是否连接。

  • 简化实现方法：

    • 将所有元素都用整数作为映射进行储存。
    • 声明时同时将元素个数确定，且创建时每个元素两两不相连。

集合列表并查集(List of Sets DS)

  • 实现结构如[{1,2,4,0},{3,5},{6}]存储的并查集
  • 缺点：线性复杂度O(N)O(N)，数据大时运行速度慢(需要迭代列表)，代码复杂

快速查找并查集(Quick Find)

  • 存储形式：
    • 单个整数列表int[]
    • 用列表的索引值映射元素内容，当元素是相互连接时，其索引值对应的列表中的元素(编号)也相同。
  • 复杂度：
    • isConnected:常数时间复杂度O(1)O(1)（只需找列表中对应索引的元素是否相同）
    • Connect:线性时间复杂度O(N)O(N)(迭代修改对应元素的编号)

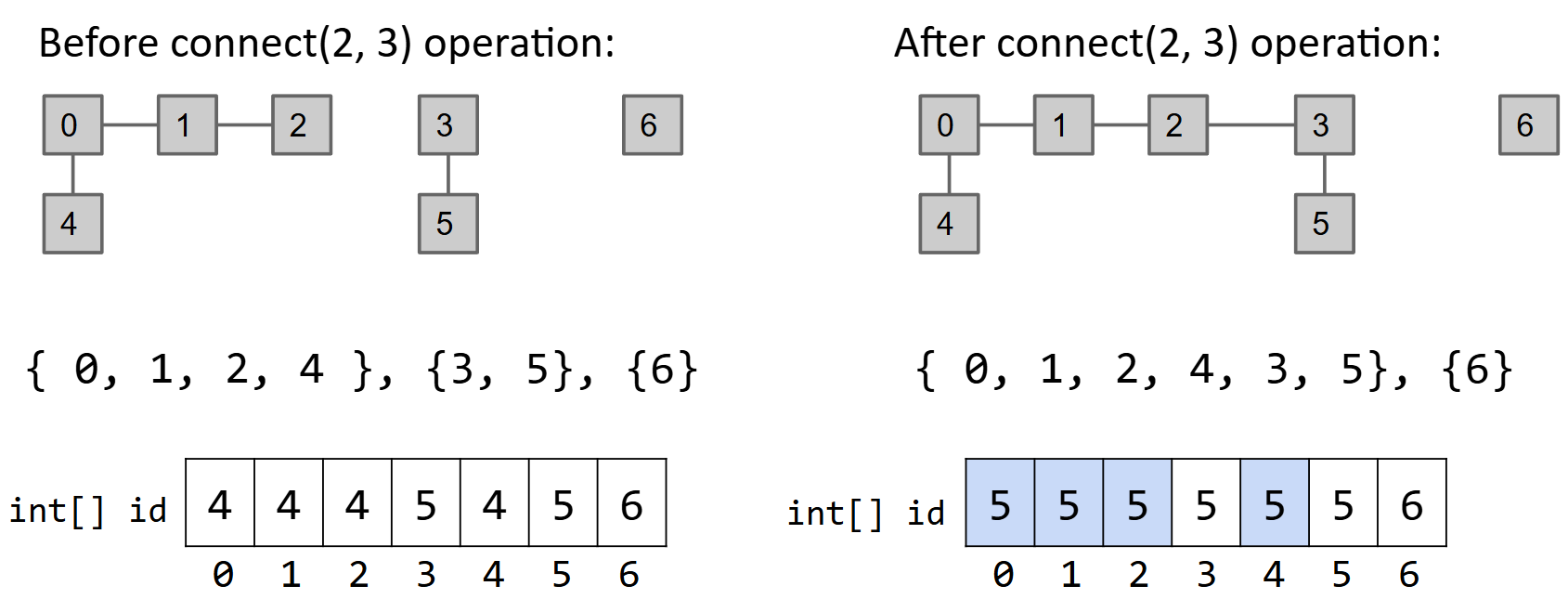
快速链接并查集(Quick Union DS)

  • 存储形式
    • int[]
    • 不同的是，列表不存储元素的编号，而是存储其的父级元素（类比树）
    • 其中，根元素存储-1表示其没有父级元素
  • 实现改进的Connect方法
    • 将一个子集链接到另一个子集时，将两个子集的根元素相连接即可。（将其中一个子集的根元素设置为另一个子集根元素的子元素）
    • O(N)O(N)
  • 实现isConnected方法
    • 检查两个元素的所在子集（树）的根元素是否相同。
    • O(N)O(N)
  • 复杂度：
    • 由树长度决定，由于connect需要爬树找到根元素，树越长，所需的时间成本越大。

加权快速并查集(Weighted Quick Union DS)

  • 加权快速连接法则
    • 当两棵树连接在一起时，始终选择较小的树放在较大的树的下面。
    • 比较树的大小而不是树的高度的原因：
      • 实际上以树的大小为权重实现的也是对数阶复杂度的方法，而代码编写难度更高一些，出于简化的原因，使用树的大小（元素个数）作为权重是完全可行的（不改变渐进复杂度）
  • 跟踪每棵树的大小的实现
    • 将列表中根元素对应的父级元素改为-size即可（size表示该树的大小）
  • 复杂度：
    • connect: O(logN)O(log{N})
    • isConnected: O(logN)O(log{N})

Better Implement:WQU DS with Path Compression

  • 路径压缩方法(Path Compression)
    • 在爬树的时候，将沿着路径上的元素都直接连接到该路径的根元素上（将路径元素的父节点直接设置为根节点），以实现树的高度的压缩。
  • 特性：随着调用方法次数的增多，下一次调用方法的时间成本会减小。
  • 复杂度（平均）：O(α(N))O(\alpha(N)),其中α(N)\alpha(N)为反阿克曼函数

算法分析

易错分析

  • 求下面函数f(N)f(N)的渐进时间复杂度
1
2
3
4
5
6
7
public static void printParty(int N){
	for(int i = 1; i <= N; i *= 2) {
		for(int j = 0; j < i ; j += 1){
			System.out.println("Hello")
		}
	}
}
  • 实际上，f(N)∉Θ(NlogN)f(N) \not \in \Theta(Nlog{N}),而是f(N)∈O(NlogN)f(N) \in O(Nlog{N})，NlogNNlog{N}只是该函数时间复杂度的上界，因为第二重循环内部的运行次数并不为NN，而是ii，而一般都是i<Ni < N，故NlogNNlog{N}只是该函数复杂度的上界
  • 事实上，f(N)∈Θ(N)f(N) \in \Theta(N)，因为1+2+4+⋯+N=2N−11+2+4+\dots+N=2N-1。

常见的复杂度计算

  • 1+2+3+⋯+N=Θ(N2)1+2+3+\dots+N=\Theta(N^2)
  • 1k+2k+3k+⋯+Nk=Θ(Nk+1)1^k+2^k+3^k+\dots+N^k=\Theta(N^{k+1})
  • k0+k1+k2+⋯+kN=Θ(kN)k^0+k^1+k^2+\dots+k^N=\Theta(k^N)
  • 1+2+4+⋯+2N=2(2N)−1=Θ(2N)1+2+4+\dots+2^N=2(2^N)-1 = \Theta(2^N)
  • 近似计算复杂度
    • ∫0Nf(x)dx≈Θ(f(N))\int_{0}^{N}{f(x)}dx \approx \Theta(f(N))

平均时间复杂度

  • 若输入的数据规模为nn，而总的运行时间为O(n)O(n),则平均下来，输入一个数据的平均运行时间为O(1)O(1)

  • 例子1：下面两个函数平均时间复杂度的比较

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//func1
public void addLast(int x) {
	if(size == items.length){
		resize(size+RFACTOR);
	}
	items[size] = x;
	size += 1;
}
//func2
public void addLast(int x) {
	if(size == items.length){
		resize(size * RFACTOR);
	}
	items[size] = x;
	size += 1;
}

  • 每个函数都执行N次后，func1的时间复杂度为Θ(N2)\Theta(N^2)，而func2为Θ(N)\Theta(N)，所以对于每次操作的平均复杂度分别为Θ(N)\Theta(N)和Θ(1)\Theta(1)，而最坏情况仍是Θ(N)\Theta(N),故后者的性能更好一些。

  • 例子2：计算下面函数的渐进时间复杂度

1
2
3
4
5
6
public static int f(int n){
	if(n <= 1){
		return 1;
	}
	return f(n-1)+f(n-1);
}
  • 试着画个图吧，你会得到答案如此f(N)∈Θ(2N)f(N)\in \Theta (2^N)的复杂度。(f(N)=1+2+4+⋯+2N−1f(N)=1+2+4+\dots+2^{N-1})
  • 基本思路
    • 对于一个已排序的数组，每次将数组从中间分为两部分，被查找的元素一定落在两部分之一(或小于中间值，或大于中间值)，故每次查找的范围是前一次的二分之一，可以实现对数阶的时间复杂度。
  • 递归实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static int binarySearch(String[] sorted,String x,int lo,int,hi){
	if(lo>hi){
		return -1;
	}
	int m = (lo+hi)/2;
	int cmp = x.compareTo(sorted[m]);
	if(cmp < 0){
		return binarySearch(sorted,x,lo,m-1); // 注意细节的减一
	} else if (cmp > 0){
		return binarySearch(sorted,x,m+1,hi); // 注意细节的加一
	} else{
		return m;
	}
}

  • 时间复杂度
    • Θ(logn)\Theta{(log n)}

归并排序(Merge sort)

  • 基本思路：
    • 将长度为NN的数组分成两个长度为N2\frac{N}{2}的数组，在子数组中进行归并排序后，再将两个子数组按序合并起来。（分治思想的体现）
  • 合并：
    • 对于两个已排序子数组，用两个不同的指针分别迭代两个数组，将两个指针指向的元素进行比较，较小者添加至新数组的末端，且指向较小者的指针向后推移一个元素，再重复此过程。
  • 复杂度分析：
    • 时间复杂度Θ(Nlog(N))\Theta(Nlog(N))
    • 分割复杂度：O(1)+O(2)+O(4)+⋯+O(N)=O(N)O(1)+O(2)+O(4)+\dots+O(N)=O(N)
    • 合并复杂度：合并需要遍历所以一次合并的复杂度是O(N)O(N)，所以从上往下每一层的时间复杂度相加可以得到总的时间复杂度（共有log2Nlog_{2}{N}层）：O(N)+O(2×N2+O(2×N4+⋯=O(N)+O(N)+⋯+O(N)=O(NlogN))O(N)+O(2\times \frac{N}{2}+O(2\times \frac{N}{4}+\dots=O(N)+O(N)+\dots+O(N)=O(NlogN))

Set&Map的特点

  • 集合(set):集合是一组项目，其中的元素没有顺序且没有重复的元素。
  • 映射(map):映射也可以叫词典，存储的是键值对，实现将键映射到值的结构。

二叉查找树(Binary Search Tree)

树的结构

  • 一棵树由若干个节点和连接节点的边组成。
  • 任意两个节点之间只能有一种连接方式（一条边），从底部到顶部只有一种方式，而不能有多种。
  • 根节点（随便一个节点都可以是根节点，没有特殊要求），可以看作是一棵树的开始。因此树是可递归的数据结构
  • 父节点：
    • 一个节点的父节点是从该节点到根节点的路径上的第一个的节点(除了本身节点)，也可以看作是一个节点的前驱。
    • 每个节点（除了根节点），都只有一个父节点。
  • 子节点：
    • 一个节点的子节点是所有以该节点作为父节点的节点。可以看作是节点的后继。
    • 一个节点可以有多个子节点。
  • 叶节点：没有子节点的节点，是树的末端节点。

二叉树(Binary Tree)

  • 特点：每个节点都只能有不超过2个的子节点。
  • 节点深度：该节点到根节点的距离（根节点为0）
  • 树高：节点深度的最大值即为树高（树高决定了最坏运行时间）

二叉搜索树(Binary Search Tree)

  • 建立在二叉树的基础上，且满足BST规则：
    • 每个节点的左子节点的值小于该节点的值。
    • 每个节点的右子节点的值大于该节点的值。
  • 且满足以下逻辑：
    • ∀x,y∈BST\forall x,y \in BST ,一定有x>y ∨ y>xx>y\space \vee \space y>x成立
    • ∀x,y,z∈BST\forall x,y,z \in BST，若$x<y \space \wedge \space y<z $ 成立，一定有 x<y<zx<y<z 成立
    • 所以不难看出，BST中没有两个相同的元素。
  • BST查找
    • 基本思路：
    • 对于一个要查找的值key，从根开始遍历，若根的元素与其相等则直接返回，若key小于根元素，则查找左子树，否则查找右子树。（递归思想）
    • 伪代码：
1
2
3
4
5
6
7
8
9
10
static BST find(BST T,Key sk){
	if(T == null)
		return null;
	if(sk.equals(T.key))
		return T;
	else if (sk < T.key)
		return find(T.left,sk);
	else
		return find(T.right,sk);
}
  • BST插入
    • 先查找树中是否已经存在，若已存在，则无需添加，若未存在，则在适当的位置创建新节点（小于一个节点的值，则进入左子树插入，反之右子树，直到遍历到叶节点时插入）
    • 伪代码：
1
2
3
4
5
6
7
8
9
static BST insert(BST T ,Key ik) {
	if(T==null)
		return new BST(ik);
	if(ik<T.key)
		T.left = insert(T.left,ik);
	else if (ik > T.key)
		T.right = insert(T.right,ik);
	return T;
}
  • BST删除
    • 删除叶节点：
      • 直接设置成null即可
    • 删除有一个子节点的节点：
      • 更改父节点的指针，使其指向该节点的子节点
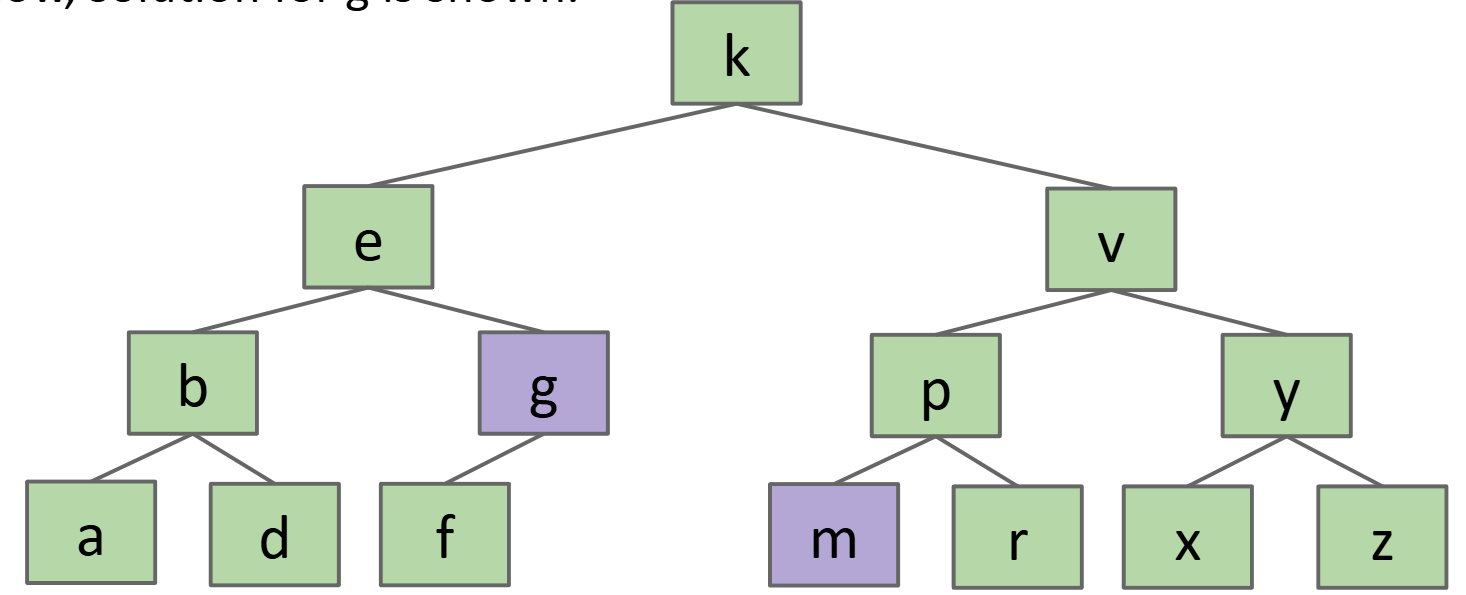
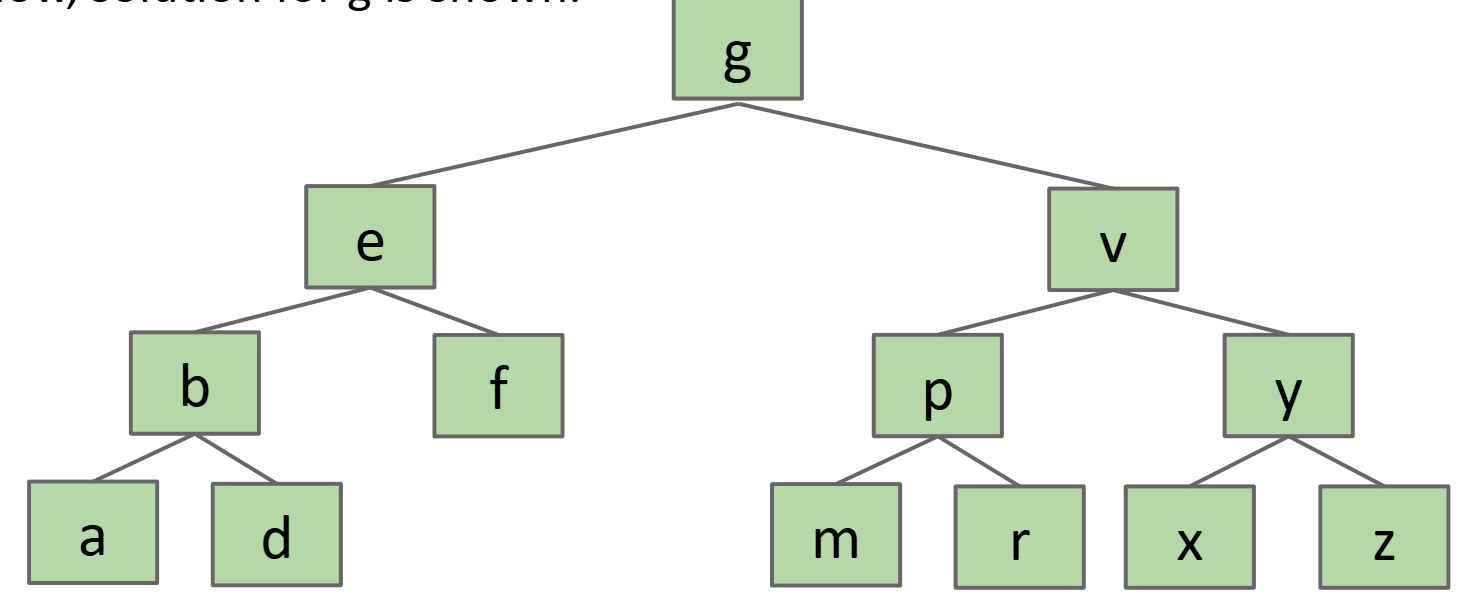
    • 删除有两个子节点的节点：
      • 找到该节点的前驱和后继(前驱：小于该节点值，且是左子树节点的最大值；后继：大于该节点值，且是右子树节点中的最小值。)
      • 用前驱或后继代替根节点。
      • 再删除原来的前驱或后继。

文件类型

  • 文件对象
    • 注意：当我们创建文件对象时，并不意味着我们创建了新的文件
1
2
3
4
5
6
7
8
9
//创建一个文件对象
File f = new File("dummy.txt");
//使用相对路径创建对象

f.createNewFile();  //创建新的文件
f.exists();         //检查文件是否已经存在
//写入文件(将文本写入对象f中)
Utils.writeContents(f,"Hello World");

  • 目录对象
    • 同理，当我们创建对象时，并没有实际在硬盘中创建目录。
1
2
3
4
// 创建一个对象
File d = new File("dummy");
//创建一个目录
d.mkdir();

Serializable（序列化）

  • 序列化是将对象转换为一系列字节的过程，这些字节可以随后存储在文件中。然后我们可以反序列化这些字节，并在程序未来的调用中获取原始对象。
  • 使用Serializable接口创建对象(注意：此接口不包含任何方法)
1
2
3
4
import java.io.Serializable;
public class Model implements Serializable {
	...
}
  • 使用Utils实现（反）序列化
1
2
3
4
5
6
7
8
Model m;
File outFile = new File("outFile.txt");
//序列化
writeObject(outfile,m);

File inFile = new File("inFile.txt")
//反序列化
m = readObject(infile,Model.class);

Lab6 通关！