CS61b:Week 9
最短路径问题
最短路径树(SPT)
- 最短路径树:从一个节点获取到其他每个节点的最短路径时,实际返回的是树的数据结构,(因为每个顶点到达它的最短路径有且只有一条)
- 若一个图的顶点数为,则其最短路径树会有()条边。(每个顶点都只有一条与之关联的边,除了源节点)
Dijkstra’s Algorithm
- 从一个源节点开始,将其他节点放入一个优先队列(确保每一次访问的节点是距离源节点最近的节点)中。
- 标记源节点,访问源节点的相邻节点,并将走过的距离记下(从源节点到该节点路径上的权总和)通过列表存储,通过键值对(节点:路程)的方式存储在优先队列中,
- 从优先队列中返回走过路程最小的节点,标记它,访问其相邻节点,并将走过的距离记下,将该节点的上一个节点记下(记录路径),若该路程小于原列表中记录的对应的路程,则进行更新(包括路程和上一个节点)。–松弛操作。
- 一直重复上述过程,直到优先队列的元素全部离队。
不变量
- 路程数组记录的一直是当前为止到对应节点的最短路程。
- 记录路径的数组记录的一直是到对应节点的最短路径的中的上一个节点。
- 优先队列包含的是尚未访问的节点(且保证其访问顺序一直是先访问距离源节点距离最近的节点)
特性
- 访问顺序是优先访问距离源节点距离最近的节点。
- 访问已经访问过的节点时一定不会更新到该节点的最短路程。
- 不适用于负权重的图中。
复杂度
- 假设图的顶点数为V,边数为E
- 时间复杂度为
- 考虑使用的数据结构为优先队列,要进行V次添加,每次添加需要;要进行V次删除最小值,每次删除需要;要进行E次调整优先级,每次调整需要,记起来即可得到总时间复杂度。
伪代码
1 | - PQ.add(source, 0) |
- 边的松弛:Relaxing an edge p → q with weight w:
1 | - If distTo[p] + w < distTo[q]: |
A* Algorithm
- 使用Dijkstra算法时,会得到到所有节点的最短路径,而如果需要的只是给定两点之间的最短路径,则会有许多不必要的开销。
- 算法只保证了起点到目标节点最短路径的正确性,而不保证其他节点最短路径的正确性。(与Dijkstra算法区分)
使用启发式函数添加惩罚
1 | //启发式函数 |
- 除了记录路程的数组以及记录路径的数组之外,新增一个存储惩罚度的数组。
- 每次优先队列考虑优先级时,优先级由最短路程+该节点的惩罚度得到。
- 靠近目标节点的节点惩罚度较小,远离目标节点的节点惩罚度大。
- 惩罚度由启发式函数得到,它将节点映射到数字。
- 可以通过乐观式低估真实成本设计启发式函数,来设计惩罚度。
- 启发式函数决定了算法的好坏。
- 启发式函数的一些标准:
- h(v, NYC) ≤ true distance from v to NYC
- For each neighbor of w:h(v, NYC) ≤ dist(v, w) + h(w, NYC).Where dist(v, w) is the weight of the edge from v to w.
最小生成树
定义:
- 生成树:一颗包含图所有顶点的树(没有环的结构)。
- 最小生成树:生成树中,各边权重总和最小的生成树。
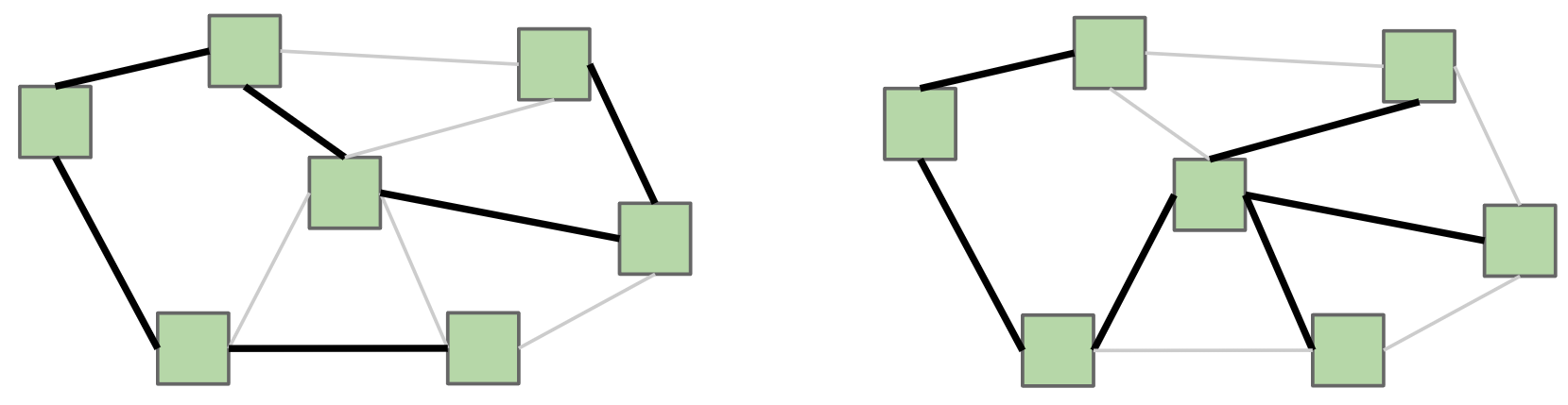
切分定理
- 切分:将图的所有顶点分为两个非空互不重叠的集合。
- 横切边:连接两个不同集合顶点的边。
- 定理:在加权图中,对于任意的切分方法,它的横切边的最小权重的边必然属于对应的最小生成树中。
Prim算法
- 随机选择一个节点做为起点,标记该节点,形成切分,取得权重最小的横切边,将其连接的另外一个节点也标记,于是又产生新的切分,取得权重最小的横切边,一直重复此过程,直到所有的节点都被标记
- 缺点:随着标记节点的不断增加,需要考虑的横切边的数量的规模不断增大,时间成本增加。
改进的Prim算法
- 与Dijkstra算法相似,引入一个优先队列,对各个节点到已建立的树的距离(实际上就是横切边的权)设置优先级,使用松弛的方法,逐步建立最小生成树。使用数组记录个节点到已建立树的距离,以及记录走过的路径。
- 复杂度:
伪代码
1 | public class PrimMST { |
Kruskal算法
- 将图中的个边根据权重从小到大的顺序排列,按顺序将边加入到构建的最小生成树中,直到加入的边会构成一个环时停止(树的边数为V-1条时)。(不加入这条边)
环判断
- 使用并查集的数据结构实现算法。
- 将所有顶点加入到并查集中,每次加入边到构建树时,在并查集将对应的元素连接。若要连接的两个元素在并查集中已经连接,则会形成环状结构。
复杂度分析
- 考虑并查集和优先队列的结构
- 优先队列中:插入E次,每次;删除最小值次,每次。
- 并查集中:连接次,每次;判断连接次,每次。
- 综上考虑,总复杂度为。(并查集对应的复杂度增长十分缓慢小于优先队列的复杂度)
有向无环图(DAG)的拓补排序
- 对于一个有向无环图,在这种排序中,图中的所有顶点被排列成一个线性序列,满足若从顶点A到顶点B有一条路径,则顶点A必须在序列中出现在顶点B之前。
- 算法:使用深度优先搜索算法后序遍历图,得到的路径倒置即可得到拓补排序。若一次深度优先搜索不能遍历整个图,则必须对其它节点开始进行深度优先搜索(不访问已经遍历过的元素)。
DAG的最短路径算法(考虑负权重)
- 与Dijkstra算法几乎相同,不同的是访问节点的顺序。
- DAG的最短路径算法按照其拓补排序的顺序访问节点,即可解决负权重的问题。
DAG的最长路径算法
- 使用数学中化归的思想,将未知问题转化成已知问题来解决。
- 将DAG中的正权重全部取相反数,即可将最长路径算法转化为最短路径算法,即化归。
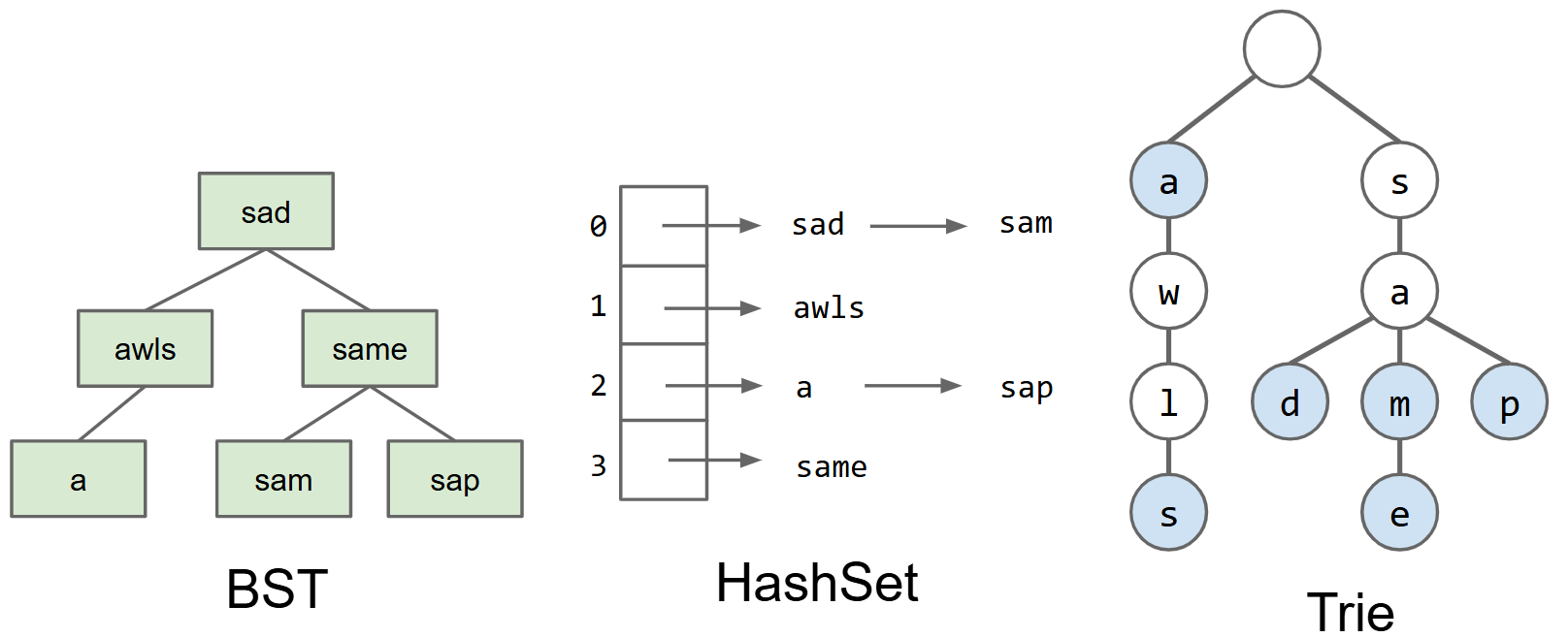
Trie(尝试树/前缀树)
索引列表
- 若一个集合只包含字母(A到Z),没有重复元素,则可以创建一个长度为26的数组只存放true/false,若集合中包含则为true,否则为false。(将字母映射到数字,存放的是)
- 将字母扩展到更一般的情况(字符,ASCII的映射),即为索引列表
- 复杂度: - ; - ,只需查看对应键的元素是true还是false即可,常数复杂度
Trie的结构
- Trie是一棵树,用于存储字符串(映射),其节点是单个字符,一个节点的父节点是其对应字符串中的上一个字符,子节点是对应字符串中的后一个字符
- 其中将字符串末尾的字符所在的节点进行标记,以确定一个字符串的重点。
- 存储字符串与整数的键值对时,只需在字符串末尾的对应节点存储该字符串对应的整数值。
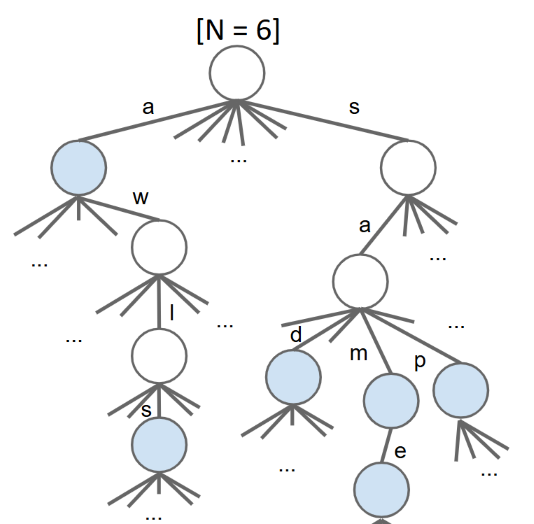
- 缺点:因为一个节点的索引数组很大,当存储节点多时,占用的内存会很大
- 改进:每一个节点不需要存储字符,因为其在它的父节点中的索引数组中的对应索引就是它的ASCII码,即已经储存了它的对应的字符。
1 | public class TrieSet { |
复杂度
- 给定一个含有个键(是键的数目,不是节点的数目,对应的是一个节点中索引列表的长度)的尝试树。
- add :
- contain :
- 尝试树的时间渐进复杂度与其存储的键的数目无关,无论其索引数组有多长,运行时间恒定
- 实际上运行时间与字符串的长度有关。(线性复杂度)
| Key Type | Get | Add | |
|---|---|---|---|
| DataIndexedArray | char | ||
| Tries | string |
索引数组的改进
- 由于索引数组的长度很大,而没有对应节点时存储null,因此会有很多重复的null储存在数组中,导致冗余。
- 改进:可以替换索引数组的数据结构,而不是使用数组,如:哈希表,BST,存储键值对(只存储存在的键值对,就不用存储重复的null)。(抽象层次up!)
Trie的特殊操作
- 可以查找所有以特定前缀开头的单词。(DFS+记录)

