数字逻辑电路入门

基本逻辑运算

逻辑运算是对逻辑变量（0，1或T，F）和逻辑运算符号的组合序列所作的逻辑推理。
基本逻辑运算
- 与(AND)：相当于逻辑运算的乘法，符号 $\wedge$
- 或(OR)：相当于逻辑运算的加法，符号 $\vee$
- 非(NOT)：代表逻辑上的否定(取反)，符号 $\neg$
- 优先级：非 > 与 = 或
- $\neg (A \vee B) = \neg A \wedge \neg B$
- $\neg(A \wedge B) = \neg A \vee \neg B$
与或非的真值表

A	B	$\neg A$	$A \wedge B$	$A \vee B$
0	0	1	0	0
0	1	1	0	1
1	0	0	0	1
1	1	0	1	1

逻辑门

晶体管

晶体管必须要在外加电源下工作，每个晶体管可以根据外部电源的变化而展现出不同的状态（通过控制晶体管的电源来控制它们开关的状态）
以NMOS三极管为例：有 $D,S,G$ 三个引脚。 $D$ 端表示高电压，通常都是 $5V$ 。 $S$ 端接地，通常为 $0V$ 。当 $G$ 输入高电压时，代表输入逻辑 $G=1$ ，晶体管导通；当 $G$ 输入低电压时，代表输入逻辑 $G=0$ ，晶体管断开。

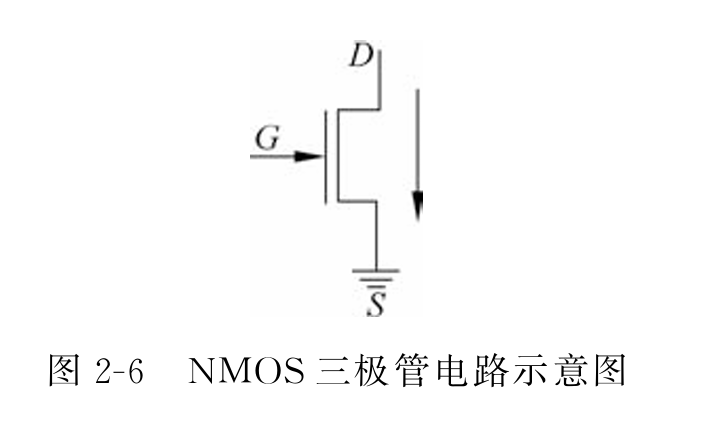
与门：把两个晶体管的输入电压串联可以实现与门
或门：把两个晶体管的输入电压并联可以实现或门
非门：通过晶体管实现，比如输入电压1,晶体管导通,输出电压的线路就接地了,只好输出0;而输入电压0,晶体管断开,输出电压的线路就变成了高电压,只好输出1。

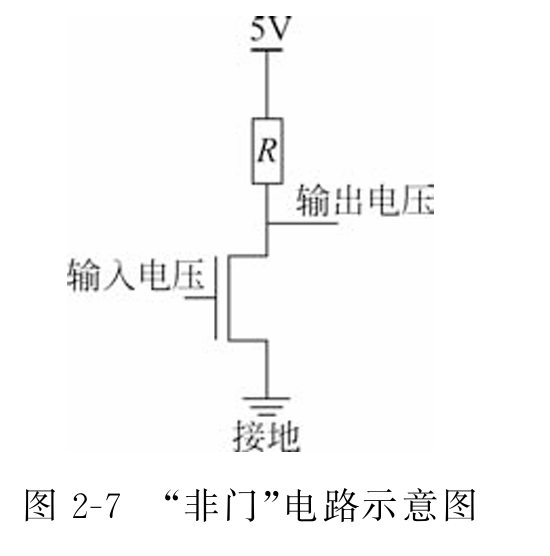
逻辑门实现加法

半加器

接受两个输入（1位的二进制数A,B），给出两个输出(得到的二进制数位，和进位)，实现不考虑进位的加法。
半加器的真值表

A	B	Sum	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

半加器的逻辑表达式（由上述真值表推出）

$SUM=\overline AB+A\overline B$

$CARRY=AB$

根据逻辑表达式就可以实现半加器的运算了

全加器

接受三个输入（两个1位的二进制数A,B,和进位C），给出两个输出（所得本位的和与进位）。
全加器的真值表

A	B	C	Sum	Carry
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

全加器的逻辑表达式

$SUM=\overline{AB}C+\overline AB\overline C+A\overline{BC}+ABC$

$Carry=\overline{A}BC+A\overline BC+AB\overline C+ABC=AB+BC+AC$

逻辑表达式的化简

基本性质（加法表示逻辑中的或运算，乘法表示与运算）
- $A+\overline A = 1$
- $1+A=A$
- $A+A=A$
- $1·A=A$
常见化简方法
- $AB+A\overline B = A(B+\overline B)=A$
- $A+AB=A(1+B)=B$
- $A+\overline AB=A+B$
- $\overline A +AB = \overline A+B$

卡诺图

定义：在逻辑代数中，卡诺图（Karnaugh map）是真值表的变形，它可以将有n个变量的逻辑函数的 $2^n$ 个最小项组织在给定的长方形表格中，同时为相邻最小项（相邻与项）运用邻接律化简提供了直观的图形工具。但是，如果需要处理的逻辑函数的自变量较多（有五个或更多的时候，此时有些项就很难圈了），那么卡诺图的行列数将迅速增加，使图形更加复杂.
特点：
- 单元格对应的最小项按格雷码摆放
- 任何两个相邻单元格对应的最小项只有一个变量取值不同
如，全加器的Carry对应的卡诺图(通过真值表填写)

C\AB	00	01	11	10
0	0	0	1	0
1	0	1	1	1

画出卡诺图后，圈出相邻的1
- 小方格的个数必须为2m,m=0,1,2…
- 圈越大越好
- 小方格可以重复使用
- 相邻：紧靠在一起的、行列首尾的、对称的(本质上：满足格雷码特点–有一位数不同即为相邻)
- 全部的1用过之后就可以停止了，每个圈代表一个与项
- 如以上的全加器的例子就可以圈出3个相邻的1
消去与项的变量：
- 观察与项的变量情况，若一个变量既可以取0又可以取1，则可以消去（对结果没贡献）
最后将所有与项相加即可化简。
- 例子的化简结果为 $Carry=BC+AB+AC$

涟波进位加法器

把多个1位全加器串联起来，将一个全加器的进位连接到与其相邻的全加器的输入进位，即可计算n位二进制的加法，这种加法器称为涟波进位加法器

数据的存储形式

信息在计算机内部以二进制的形式存储
一个二进制位数（0或1）占用1位（bit，b），每连续的8位为1个字节（Byte，B），CPU读取数据的最小单元是字节。
计算机存储常用的单位：
- $1KB(KiloByte)=1024B=2^{10}B$ ， $1MB(MegaByte)=1024KB$ ， $1GB(GigaByte)=1024MB$ ， $1TB(TeraByte)=1024GB$ ， $1PB(PetaByte)=1024TB$ ， $1EB(ExaByte)=1024PB$
- 十进制下：
- $K=10^3,M=10^6,G=10^9,T=10^{12},P=10^{15},E=10^{18}$
- 二进制下：
- $K=2^{10},M=2^{20},G=2^{30},T=2^{40},P=2^{50}, E=2^{60}$
字符采用二进制编码存储，常见的字符编码如下：
- ASCII字符编码
- UNICOTE字符编码

小练习

实现比较器 (comparator)：
if X>=Y then out=1; else out=0 where X, Y are two-bit binary numbers.
也就是输入(a,b,c,d) 四位元, 其中ab两位元代表X， cd俩位元代表Y。
例如当（abcd）= (0100) 时，代表X=01, Y=00, 则X>=Y, 所以out=1.
A. 写出比较器输入(abcd),输出out的真值表(truth table).
B. 写出对应真值表的sum-of-products.
C. 用卡诺图(K map)简化前面B的sum-of-products.
D. 用python的逻辑运算and, ,or, not 实现简化后的结果来完成comp(a,b,c,d)函数。
E. 试验comp(0,1,1,0), comp(1,1,1,0), comp(0,1,0,1), comp(0,1,1,1), comp(0,0,0,0).
参考代码

def comp(a,b,c,d):
    p1 = (a and b)
    p2 = (not c and not d)
    p3 = (b and not c)
    p4 = (a and not c)
    p5 = (a and not d)

    return  p1 or p2 or p3 or p4 or p5 

print(int(comp(0,1,1,0)))
print(int(comp(1,1,1,0)))
print(int(comp(0,1,0,1)))
print(int(comp(0,1,1,1)))
print(int(comp(0,0,0,0)))
#输出
#0
#1
#1
#0
#1

我的做法：
真值表：

a	b	c	d	result
0	0	0	0	1
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	1
0	1	0	1	1
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

卡诺图：

cd\ab	00	01	10	11
00	1	1	1	1
01	0	1	1	1
10	0	0	1	0
11	0	0	1	1

由卡诺图得到化简表达式：(5个圈圈就可以啦)

$CMP=\overline{CD}+AB+B\overline C+A\overline C+A\overline D$

a	b	c	d	result
0	0	0	0	1
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	1
0	1	0	1	1
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

a	b	c	d	result
0	0	0	0	1
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	1
0	1	0	1	1
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

a	b	c	d	result
0	0	0	0	1
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	1
0	1	0	1	1
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1